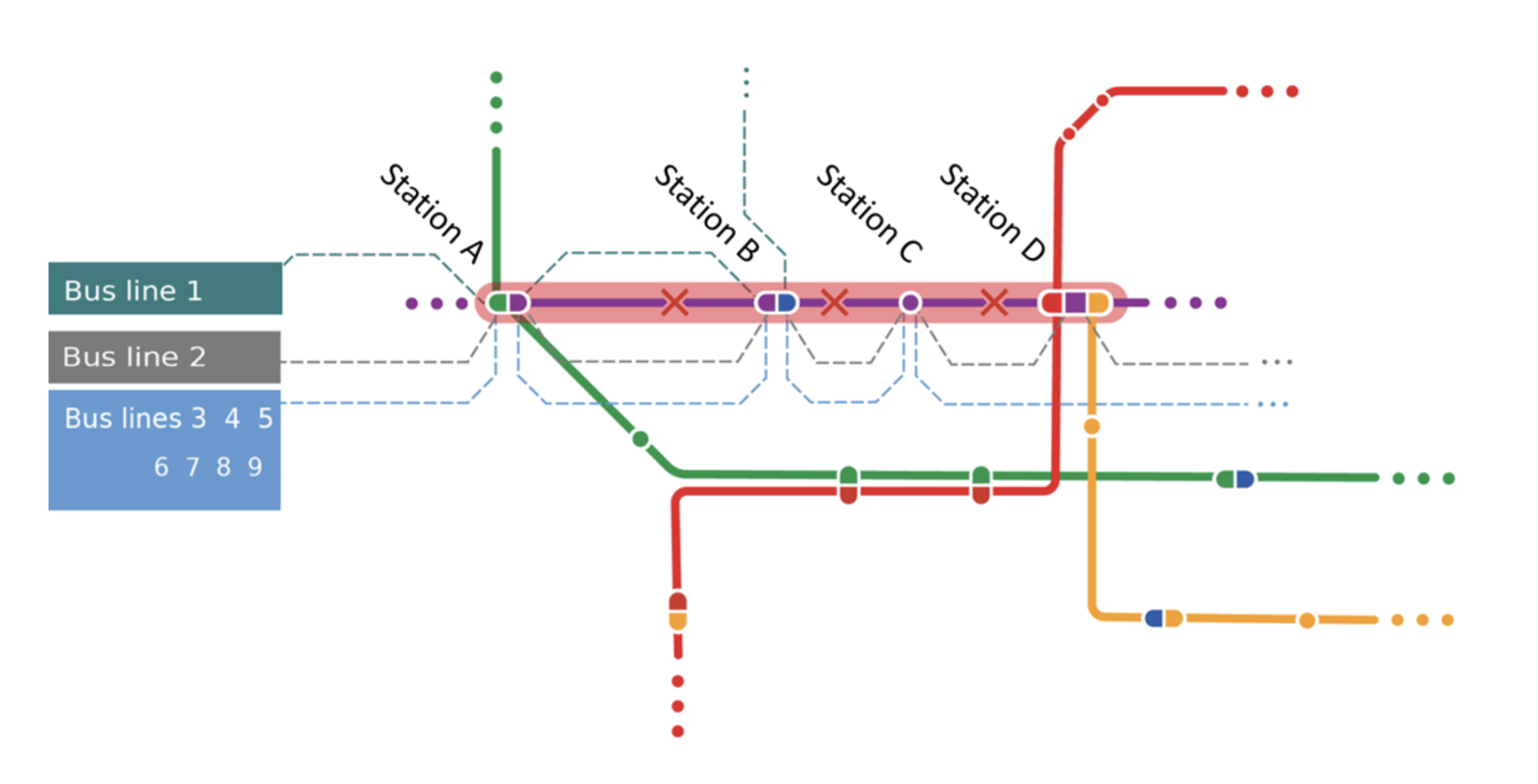
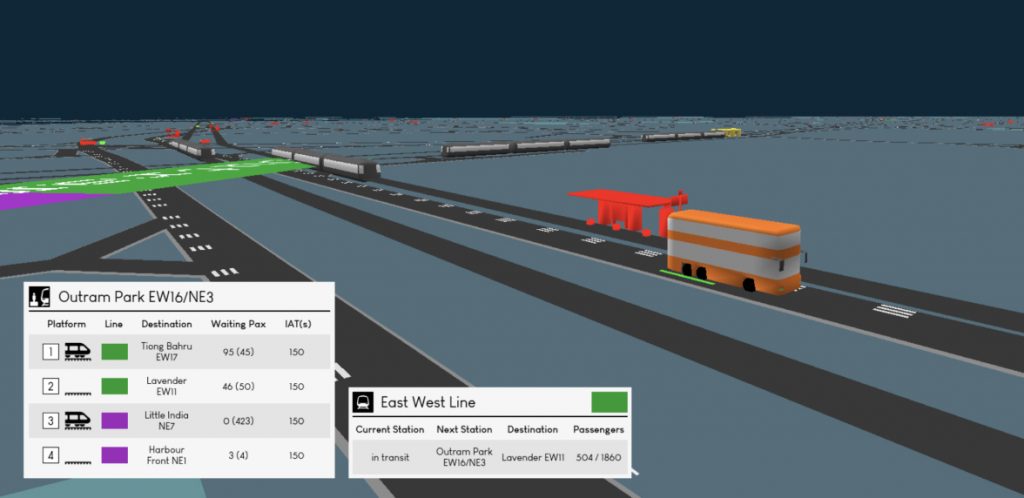
In the domains of fleet management and transport planning, often numerical optimisation is used to find an optimal solution to a given complex problem. These problems commonly include the assignment of vehicles to tasks under given constraints, the optimisation of routes, as well as finding the minimum resources required to fulfil a list of given requirements. The scenario as well as
the problem is formulated using mathematical equations which can then be solved using modern solvers such as CPLEX. For these optimisation problems to be manageable, they usually need to be simplified. Also, complex human behaviour and their interdependencies need to be expressed mathematically which also requires significant simplification, often to the extent where the validity of the obtained results can be questioned.
The combination of optimisation with a realistic simulator to study the feasibility, validity and efficacy of a proposed solution, or, in the case of multi-objective optimisation, a pareto set, significantly increases the fidelity and trustworthiness of the entire approach. Insights gained with the simulation can be fed back into the optimisation model (e.g., assumed travel times of buses) and, where possible, new constraints can be included to avoid finding solutions that would only work in the mathematical representation of the real world, but not in the real world itself.